|
تفریح با ریاضی بانک سوالات-معما-هوش-
| ||
|
|
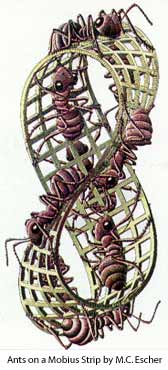
نوار موبیوس نواری است که دو لبة آن بر هم قرار گرفته و حلقهای را به وجود میآورد؛ البته باید یک لبة انتهایی قبل از اتصال به لبة دیگر نیم دور چرخانده شود. این نوار را دو ریاضیدان آلمانی به نامهای آگوست فردیناند موبیوس و جان بندیکت (Johann Benedict) در سال ۱۸۵۸ به طور مستقل و جداگانه کشف کردند و به ثبت رساندند.
◄ روش ساخت نوار موبیوس:
ابتداییترین راه برای ایجاد این نوار، انتخاب یک نوار مستطیل شکل، دراز و نرمی است که آن را یک بار میپیچانیم و سپس دو انتهای آن را به هم متصل میکنیم. سطحی که به این ترتیب به دست میآید «نوار موبیوس» نامیده میشود.
این سطح تنها یک رو دارد. به بیان دیگر، یک صفحة کاغذی را میتوان با دو رنگ گوناگون در دو طرف آن رنگ کرد اما نوار موبیوس را با این روش نمیتوان با دو رنگ مختلف رنگ کرد. در صورت اقدام به چنین کاری به همان جایی که رنگ کردن را در ابتدا آغاز کرده بودیم، میرسیم؛ در حالی که در طرف دیگر نوار هستیم! پس نوار موبیوس، سطحی است که یک رو دارد و حرکت ما روی آن تا بینهاِت بار تکرار می شود. ◄ تعریف خاص ریاضی: دلیل «یک رویه بودن» این نوار آن است که در هر نقطة a از نوار موبیوس میتوان دو بردار با جهتهای مختلف رسم کرد که بر نوار موبیوس در این نقطه عمود باشد. این بردارها را قائمهای نوار موبیوس در نقطة a مینامیم. یکی از این بردارها را انتخاب و نقطة a را به تدریج روی نوار موبیوس جابجا میکنیم. در این صورت بردار ما هم همراه با نقطه a جابجا میشود. بنابراین، روی نوار موبیوس چنان مسیر بستهای وجود دارد که اگر قائمی این مسیر را روی سطح بپیماید، به جای این که به وضع نخستین خود برسد، روی برداری که در جهت مخالف وضع نخستین آن است قرار میگیرد. بخش دوم: مفهوم مرز ناحیه، خواص و کاربرد نوار موبیوس
◄ روش ساخت نوار موبیوس:
ابتداییترین راه برای ایجاد این نوار، انتخاب یک نوار مستطیل شکل، دراز و نرمی است که آن را یک بار میپیچانیم و سپس دو انتهای آن را به هم متصل میکنیم. سطحی که به این ترتیب به دست میآید «نوار موبیوس» نامیده میشود.
این سطح تنها یک رو دارد. به بیان دیگر، یک صفحة کاغذی را میتوان با دو رنگ گوناگون در دو طرف آن رنگ کرد اما نوار موبیوس را با این روش نمیتوان با دو رنگ مختلف رنگ کرد. در صورت اقدام به چنین کاری به همان جایی که رنگ کردن را در ابتدا آغاز کرده بودیم، میرسیم؛ در حالی که در طرف دیگر نوار هستیم! پس نوار موبیوس، سطحی است که یک رو دارد و حرکت ما روی آن تا بینهاِت بار تکرار می شود. ◄ تعریف خاص ریاضی: دلیل «یک رویه بودن» این نوار آن است که در هر نقطة a از نوار موبیوس میتوان دو بردار با جهتهای مختلف رسم کرد که بر نوار موبیوس در این نقطه عمود باشد. این بردارها را قائمهای نوار موبیوس در نقطة a مینامیم. یکی از این بردارها را انتخاب و نقطة a را به تدریج روی نوار موبیوس جابجا میکنیم. در این صورت بردار ما هم همراه با نقطه a جابجا میشود. بنابراین، روی نوار موبیوس چنان مسیر بستهای وجود دارد که اگر قائمی این مسیر را روی سطح بپیماید، به جای این که به وضع نخستین خود برسد، روی برداری که در جهت مخالف وضع نخستین آن است قرار میگیرد. بخش دوم: مفهوم مرز ناحیه، خواص و کاربرد نوار موبیوس
برچسبها: |
|
| [ طراحی : پرشین اسکین ] [ Weblog Themes By : Persian Skin ] | ||